Задача 1.1. Для представленной электрической схемы определить токи во всех ветвях схемы методом контурных токов.
  Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей.
Решение:
Определяем количество независимых контуров и обозначаем их контурные токи. Далее составляем систему уравнений для первого, второго и третьего контуров по второму закону Кирхгофа.
Кому интересна теория составления системы уравнений - могут открыть сноску, находящуюся ниже.
теория метода контурных токов
При расчете цепей методом контурных токов принимается, что в каждом независимом контуре цепи течет свой контурный ток. Для определения этих токов составляют уравнения по второму закону Кирхгофа. Число независимых контуров определяется как К = В - Y + 1, где В - число ветвей, Y - число узлов. В нашем случае на представленной схеме мы имеем шесть ветвей (первая через через резистор R1, вторая - через R2 и r2, треться - через R3 и r3, четвертая через R4, пятая через R5 и шестая ветвь проходит через R6). Узлов (параметр Y) в схеме - четыре (по количеству пересечений соединяемых проводов - на схеме показаны точками). Таким образом, посчитав, получим количество независимых контуров - три: К = 6 - 4 + 1 = 3. Количество независимых контуров соответствует требуемому количеству уравнений в составляемой системе. Впрочем, количество независимых контуров можно определить визуально по схеме. Каждый контур должен быть в своих границах и не "залезать" в соседний. Независимые контуры можно обозначить римскими цифрами, а замыкающиеся в них контурные токи отметить индексами, соответствующими своему контуру (I11, I22, I33). Для единообразия все контурные токи можно направить в одну сторону, например, по направлению часовой стрелки, но принципиального значения это не имеет. Иногда визуально удобнее их направлять по направлению полярности источника ЭДС, там, где этот источник в контур входит. А если он в контуре не один, то в любом направлении. На правильности вычисления это никак не скажется. При составлении уравнений по методу контурных токов, следует учитывать, что в контурах, где имеются источники ЭДС, численные значения этих ЭДС необходимо принимать положительными, если их направление совпадает с выбранным направлением контурного тока, и отрицательными, если их направление не совпадает с выбранным направлением контурного тока. Решая совместно уравнения, составленные по второму закону Кирхгофа, находят величины контурных токов. Токи в ветвях цепи находятся через контурные токи по методу наложения.
|
А мы решаем дальше...

Пояснения к первому уравнению: в своем замкнутом контуре №1 контурный ток I11 без учета воздействия других контурных токов как бы "соберет" все сопротивления в этом контуре под знак "плюс". Однако, ток I33 в третьем контуре пройдет в обратном направлении через сопротивление R4 по сравнению с током первого контура через это же сопротивление, поэтому из произведение запишется со знаком "минус". А вот контурный ток I22 второго контура пройдет через сопротивление R1 в том же направлении, что и контурный ток первого контура через это же сопротивление. А значит присоединится к нам их произведение со знаком "плюс". Все слагаемые представляют из себя произведение тока на сопротивление, т.е. - это напряжение. И сумма этих слагаемых, т.е. напряжений данного контура должна равняться ЭДС, входящей в данный контур. А это по условию 110В.
Также составляются с учетом положительных и отрицательных знаков уравнения и для других контуров.
Учитывая исходные данные, запишем систему для контурных токов к виду попроще, причем контурные токи расположим для удобства по порядку и с учетом их знаков, полученных ранее.
 Далее придется, как это ни грустно Далее придется, как это ни грустно , заняться математикой. Домножим второе уравнение (при умножении обоих частей равенства на одно и тоже число или при делении - равенство не нарушается) на три и сложим его с третьим уравнением. Это позволит нам избавиться от одного неизвестного, а именно контурного тока контура №1. Третье же уравнение перепишем без изменений. , заняться математикой. Домножим второе уравнение (при умножении обоих частей равенства на одно и тоже число или при делении - равенство не нарушается) на три и сложим его с третьим уравнением. Это позволит нам избавиться от одного неизвестного, а именно контурного тока контура №1. Третье же уравнение перепишем без изменений.
решаем дальше...

После домножения второго уравнения на три и сложения второго и третьего получим:

Чтобы избавиться от больших чисел, просто для удобства вычислений, можно каждое из уравнений разделить на 10. Тогда получим:

Из второго уравнения выразим I22. Получим, что 
Теперь это значение (вместо I22) можно подставить в первое и третье уравнение. Это даст нам возможность избавиться от одного неизвестного и перейти к системе из двух уравнений вместо трех:

Раскрыв скобки и сложив одинаковые слагаемые, получим:
Умножим обе части второго уравнения на два и сложим с первым уравнением. Это позволит нам избавиться еще от одного неизвестного, а именно I11. И мы получим простое уравнение с одним неизвестным:  . Откуда . Откуда  - это контурный ток третьего контура. - это контурный ток третьего контура.
Теперь из этого уравнения  возьмем второе и подставим в него полученное значение контурного тока третьего контура. После подстановки получим, что возьмем второе и подставим в него полученное значение контурного тока третьего контура. После подстановки получим, что 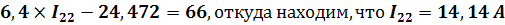 - контурный ток второго контура. - контурный ток второго контура.
Теперь в первое уравнение системы  можно подставить найденные значения второго и третьего контурного тока и найти первый контурный ток. Подставив и посчитав, получим: можно подставить найденные значения второго и третьего контурного тока и найти первый контурный ток. Подставив и посчитав, получим:
Значения контурного тока третьего контура мы получили со знаком "минус". Значения это не имеет. Если бы на рисунке мы выбрали его направление в другую сторону, то значения при вычислении получились бы те же, но со знаком "плюс". Теперь снова смотрим на схему с выбранным направлением контурных токов и начинаем вычислять все токи через все резисторы (внутренние сопротивления источников нас не интересуют, ибо через r2 ток тот же, что будет и через R2, а через r3 ток тот же, что будет и через R3.
Через резистор R1 и первый и второй контурные токи пройдут в одном направлении, поэтому общий ток через него определится их сложением. Получаем: I1 = I11 + I22 = 4,625 + 14,14 = 18,765 A. Получили I1 = 18,765 A. Через резистор R2 пройдет только контурный ток I11, поэтому I2 = I11 = 4,625 А. Через R3 пройдет только второй контурный ток, поэтому I3 = I22 = 14,14 A. Через R4 контурный ток I33 пройдет против направления контурного тока I11, поэтому I4 = I11 - I33 = 4,625 - (- 4,37) = 8,995 А. Через R5 пройдет только третий контурный ток, поэтому I5 = I33 = - 4,37 A, т.е. на схеме его фактическое направление будет противоположно направлению контурного тока. Через R6 второй и третий контурные токи пройдут в одном направлении, поэтому I6 =I22 + I33 = 14,14 + (- 4,37) = 9,77 A. Собственно, вот все токи и нашли.
 Теперь составим баланс мощностей. Если все токи мы вычислили правильно - обе части равенства будут равны. Но может быть небольшая погрешность (около 5%) из-за того, что все значения токов приняли не целые значения, а мы их округляли в процессе вычислений. Уравнение энергетического баланса при питании только от источников ЭДС записывается следующим образом: Теперь составим баланс мощностей. Если все токи мы вычислили правильно - обе части равенства будут равны. Но может быть небольшая погрешность (около 5%) из-за того, что все значения токов приняли не целые значения, а мы их округляли в процессе вычислений. Уравнение энергетического баланса при питании только от источников ЭДС записывается следующим образом:

Если через источник ЭДС течет ток, направление которого совпадает с направлением ЭДС, то источник ЭДС отдает энергию и его мощность E*I записывается в левую часть уравнения энергетического баланса с положительным знаком. Если же ток I направлен навстречу ЭДС, то источник ЭДС работает как потребитель энергии, и его мощность записывается в левую часть уравнения с отрицательным знаком. Получаем:

Реальное направление токов в заданной схеме с учетом вычислений показано на рисунке выше.
|
Задача 2.1. Решить предыдущую задачу методом узловых потенциалов.
  Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей. Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей.
Решение:
Для начала необходимо составить уравнения по закону Кирхгофа. При расчете сложной цепи с составлением уравнений по закону Кирхгофа выбирают произвольно (обратите внимание - произвольно) направление токов в ветвях. Решая предыдущую задачу, мы выяснили истинное направление всех токов в данной схеме, поэтому для интереса просто изменили направление тока I1, чтобы показать, что результат отт выбора направлений не изменится. Как и в предыдущей задаче, если значение тока получится положительным - значит истинное направление совпадает с произвольно выбранным. Если получится отрицательным - значит истинное направление противоположно выбранному. Только и всего.
Число независимых узловых уравнений, составленных по первому закону Кирхгофа должно быть на единицу меньше числа узлов схемы. Число независимых уравнений, составленных по второму закону Кирхгофа должно быть равно числу независимых контуров. В итоге общее число уравнений должно быть равно числу искомых неизвестных
теория метода узловых потенциалов
В этом методе за неизвестные принимаются потенциалы узлов схемы - узловые потенциалы. Известно, что одна любая точка схемы может быть заземлена без изменения токораспределения в схеме. Поэтому один из узлов схемы нужно мысленно заземлить, т.е. принять его потенциал равным нулю. При этом число неизвестных в методе узловых потенциалов равно числу уравнений, которые могут быть составлены для схемы по первому закону Кирхгофа. После определения потенциалов узлов токи в ветвях рассчитываются по закону Ома. Для ветвей с источниками ЭДС ток вычисляется по формуле:
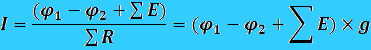
где (φ1 - φ2) - разность потенциалов узлов, к которым подключена ветвь; ΣЕ - алгебраическая сумма ЭДС ветви; ΣR - арифметическая сумма сопротивлений, включенных в данную ветвь; g = 1/ΣR - проводимость ветви.
|
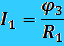 ; ; ; ; ; ;  ; ;  ; ; 
Составим уравнения по закону Кирхгофа для трех узлов. При этом ток, входящий в узел будем записывать со знаком "плюс", а выходящий со знаком "минус". Можно и наоборот - значения не имеет. Получим:
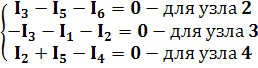
Теперь подставим в эту систему вышенайденные значения для вычисления токов. Получим следующую систему для решения нашей задачи:

Далее мы приводим все выражения к общему знаменателю 12, приводим в каждом выражении подобные слагаемые и в получившейся системе уравнений первое из них домножаем на 5,5 и складываем со вторым. Получаем:

Сложив первое уравнение со вторым и переписав два последних, получим следующую систему уравнений:
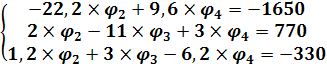
Из первого уравнения находим, что 
Подставив найденное значение во второе и третье уравнения системы, приведем подобные слагаемые и таким образом перейдем к системе уже из двух уравнений с двумя неизвестными:
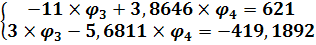
Теперь домножим первое уравнение ситемы на три, а второе на одиннадцать и сложим их. Таким образом получим уравнение с одним неизвестным:
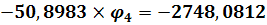 , откуда находим, что , откуда находим, что 
Подставив данное значение в любое из двух уравнений последней системы, получим, что 
Оставшееся неизвестным значение потенциала φ2 находится подстановкой вышенайденных потенциалов φ3 и φ4 в любую систему из трех уравнений. Посчитав, получится, что φ2 = 97,672. Далее по ранее определенным нами формулам для нахождения токов в ветвях находим, что:
 Как видите, значение тока первой ветви I1 получилось отрицательным. Т.е. на самом деле он будет протекать в противоположном напрвлении по сравнению с тем, которое мы выбрали в начале задачи. Точно также по остальным формулам Как видите, значение тока первой ветви I1 получилось отрицательным. Т.е. на самом деле он будет протекать в противоположном напрвлении по сравнению с тем, которое мы выбрали в начале задачи. Точно также по остальным формулам
 ; ; ; ;  ; ;  ; ;  находятся и остальные токи. находятся и остальные токи.
Получим, что I2 = 4,6307A; I3 = 14,1403A; I4 = 8,9986A; I5 = 4,368A; I6 = 9,7672A. Вывод: значения почти одинаковые и нет разницы, каким именно способом решать задачу.
Задача 3.1. Решить задачу с применением законов Ома и методом узловых потенциалов. Начертить потенциальную диаграмму контура, не содержащего ЭДС. Исходная схема представлена ниже.
  Исходные данные: Напряжение источника питания Е = 20В, сопротивления R1 = 3 Ома, R2 = 6 Ом, R3 = 4 Ома, R4 = 8 Ом, R5 = 10 Ом. Исходные данные: Напряжение источника питания Е = 20В, сопротивления R1 = 3 Ома, R2 = 6 Ом, R3 = 4 Ома, R4 = 8 Ом, R5 = 10 Ом.
Решение:
Самое простое решение - это упростить схему и решить задачу применением законов Ома. Поскольку каждые из 2-х сопротивлений R1 и R4, а также R2 и R5 включены последовательно, то их значения можно сложить и получить преобразованную схему более простого вида для лучшего понимания и удобства вычисления. Ее вид на рисунке справа. Из схемы видно, что сопротивления R1,4 и R2,5 соединены параллельно. Поэтому, посчитав их общее сопротивление по формуле результирующего сопротивления 2-х параллельно включенных резисторов и учитывая тот факт, что это сопротивление будет последовательно включено с резистором R3, получим общее сопротивление всей электрической цепи (пренебрегая внутренним сопротивлением источника питания): Получаем, что Rобщ = 10,5185 Ом. Соответственно, общий ток I1 всей цепи по закону Ома составит: I1 = E/Rобщ = 1,9014А. Далее находим токи отдельных ветвей: Получаем, что Rобщ = 10,5185 Ом. Соответственно, общий ток I1 всей цепи по закону Ома составит: I1 = E/Rобщ = 1,9014А. Далее находим токи отдельных ветвей: . Соответственно, . Соответственно, . .
Решим эту же задачу методом узловых потенциалов.
 В данном случае примем за нулевой потенциал второго узла, т.е. φ2 = 0 (можно и первый - значения не имеет) и воспользуемся формулой межузлового напряжения: В данном случае примем за нулевой потенциал второго узла, т.е. φ2 = 0 (можно и первый - значения не имеет) и воспользуемся формулой межузлового напряжения: Применительно к нашей задаче, получим: Применительно к нашей задаче, получим:  Токи ветвей составят: Токи ветвей составят:   Как видно, из двух методов решения мы пришли к одинаковым результатам. Как видно, из двух методов решения мы пришли к одинаковым результатам.
 Для построения потенциальной диаграммы нам необходимо найти потенцалы всех точек №№1,2,3,4. Начнем обходить левый контур по часовой стрелке от точки №2 до точки №2 - по замкнутому кругу. Потенциал точки №2 в начале решения мы приняли равным нулю, т.е. φ2 = 0. Находим далее: Для построения потенциальной диаграммы нам необходимо найти потенцалы всех точек №№1,2,3,4. Начнем обходить левый контур по часовой стрелке от точки №2 до точки №2 - по замкнутому кругу. Потенциал точки №2 в начале решения мы приняли равным нулю, т.е. φ2 = 0. Находим далее:  → → → → → → В идеале потенциал φ2 должен был получиться нулю, но из-за округлений в промежуточных вычислениях образовалась небольшая погрешность, но это не страшно. Округлив полученные значения потенциалов до сотых долей можно прийти к идеальному нулю. Потенциальная диаграмма строится просто - по оси Х откладываются сопротивления, концам которых соответствуют точки №№1,2,3,4, а по оси Y - соответствующие этим точкам значения вычисленных потенциалов в этих точках. В идеале потенциал φ2 должен был получиться нулю, но из-за округлений в промежуточных вычислениях образовалась небольшая погрешность, но это не страшно. Округлив полученные значения потенциалов до сотых долей можно прийти к идеальному нулю. Потенциальная диаграмма строится просто - по оси Х откладываются сопротивления, концам которых соответствуют точки №№1,2,3,4, а по оси Y - соответствующие этим точкам значения вычисленных потенциалов в этих точках.
|

 Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей.
Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей. 


 Далее придется, как это ни грустно
Далее придется, как это ни грустно


 Теперь составим баланс мощностей. Если все токи мы вычислили правильно - обе части равенства будут равны. Но может быть небольшая погрешность (около 5%) из-за того, что все значения токов приняли не целые значения, а мы их округляли в процессе вычислений. Уравнение энергетического баланса при питании только от источников ЭДС записывается следующим образом:
Теперь составим баланс мощностей. Если все токи мы вычислили правильно - обе части равенства будут равны. Но может быть небольшая погрешность (около 5%) из-за того, что все значения токов приняли не целые значения, а мы их округляли в процессе вычислений. Уравнение энергетического баланса при питании только от источников ЭДС записывается следующим образом: Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей.
Исходные данные: сопротивление нагрузочных резисторов - R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) - r2 = 1Ом, r3 = 2Ом. ЭДС источников питания - Е2 = 110В, Е3 = 220В. Составить баланс мощностей.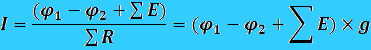
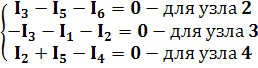


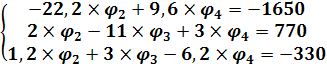

 Исходные данные: Напряжение источника питания Е = 20В, сопротивления R1 = 3 Ома, R2 = 6 Ом, R3 = 4 Ома, R4 = 8 Ом, R5 = 10 Ом.
Исходные данные: Напряжение источника питания Е = 20В, сопротивления R1 = 3 Ома, R2 = 6 Ом, R3 = 4 Ома, R4 = 8 Ом, R5 = 10 Ом. Получаем, что
Получаем, что  . Соответственно,
. Соответственно, .
. В данном случае примем за нулевой потенциал второго узла, т.е. φ2 = 0 (можно и первый - значения не имеет) и воспользуемся формулой межузлового напряжения:
В данном случае примем за нулевой потенциал второго узла, т.е. φ2 = 0 (можно и первый - значения не имеет) и воспользуемся формулой межузлового напряжения: Применительно к нашей задаче, получим:
Применительно к нашей задаче, получим:  Токи ветвей составят:
Токи ветвей составят: Для построения потенциальной диаграммы нам необходимо найти потенцалы всех точек №№1,2,3,4. Начнем обходить левый контур по часовой стрелке от точки №2 до точки №2 - по замкнутому кругу. Потенциал точки №2 в начале решения мы приняли равным нулю, т.е. φ2 = 0. Находим далее:
Для построения потенциальной диаграммы нам необходимо найти потенцалы всех точек №№1,2,3,4. Начнем обходить левый контур по часовой стрелке от точки №2 до точки №2 - по замкнутому кругу. Потенциал точки №2 в начале решения мы приняли равным нулю, т.е. φ2 = 0. Находим далее: 

 1. Изображаем схему замещения соответствующего режима холостого хода:
1. Изображаем схему замещения соответствующего режима холостого хода:


 Изображаем схему замещения соответствующего режима короткого замыкания:
Изображаем схему замещения соответствующего режима короткого замыкания:




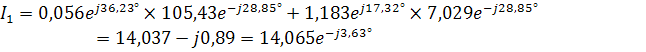
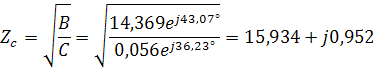 Проверить можно как
Проверить можно как 


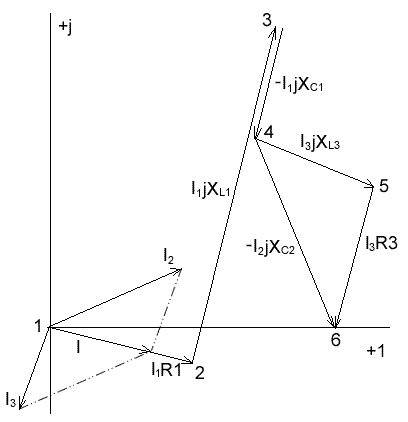
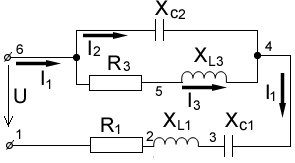 Записываем комплексы сопротивлений:
Записываем комплексы сопротивлений:
