Задача 1. Определить общее сопротивление электрической цепи, напряжение и мощность каждого проводника на рис.1 при R1 = 10Ом, R2 = 25Ом, R3 = 15Ом и R4 = 14Ом. Напряжение источника напряжения U = 16В. Внутренним сопротивлением источника пренебречь.
Задача 2. В домашнюю розетку через удлинитель включены холодильник мощностью 300Вт, стиральная машина мощностью 2,5кВт и СВЧ-печь мощностью 1,5кВт. Определить общий ток в цепи и ток каждого из потребителей. Решение: Составим электричесую схему включения потребителей. Она представлена на рис.2 и будеть представлять из себя параллельное включение проводников(см. рис.4 в разделе "Про сопротивление"). Токи приборов вычислим из формулы определения мощности: P = U*I откуда I = P/U.
Решение: Поскольку лампы имеют меньшее напряжение, чем напряжение сети, их необходимо соединить последовательно. Поскольку параметры их одинаковы, необходимо общее напряжение разделить на рабочее напряжение ламп. Получим: N = 220/3,5 = 62,86(штук). Округляем до целого значения: N = 63 штуки.
Задача 2.2. Требуется рассчитать напряжение на каждой из ламп подобно рис.3, но с учетом того, что одна лампа перегорела и ее заменили на лампу с параметрами U = 3,5В и током I = 0,26А. Остальные лампы на то же напряжение, но рабочий ток I = 0,16А. Рассчитать мощности этих двух типов лампочек. Решение: Мощности находим по формуле Р = U*I. Получим: Р1 = U1*I1 = 3,5*0,26 = 0,91Вт; Р2 = U2*I2 = 3,5*0,16 = 0,56Вт. Общий ток в цепи найдем при предварительном нахождении общего сопротивлении всей цепи. Сопротивление первого типа лампы R1 = U1/I1 = 3,5/0,26 = 13,46Ом. Второго типа: R2 = U2/I2 = 3,5/0,16 = 21,875Ом. Общее сопротивление: R = R1 + R2*62 = 13,46 + 1356,25 = 1369,71Ом. Ток в цепи составит: I = U/R = 220/1369,71 = 0,1606 А. Тогда напряжение на первом типе лампы составит U1 = I*R1 = 0,1606*13,46 = 2,16В. На втором типе U2 = I*R2 = 0,1606*21,875 = 3,51В. Задача 3.1. Имеется гараж, освещение которого состоит из последовательно соединенных ламп в количестве 20штук рабочим напряжением 12В и мощностью 40Вт каждая. Через какое-то время хозяин заменил половину, т.е. 10шт, из них на более мощные с тем же рабочим напряжением , но по 60Вт. Однако, после такой замены оставшиеся лампы мощностью 40Вт стали перегорать чаще. Могло ли так стать и почему, ведь общее их количество не изменилось, а половина из них даже мощнее, чем по 40Вт?
Попробуем разобраться. Мысленно представим себе гирлянду из 20ламп на 12В питающихся от 220В. По сути - это тот же рис.4 в задаче выше, только с другими параметрами ламп. Поскольку лампы включены последовательно, значит и сопротивления их нитей накала включены также. В таком случае, рассчитаем общее сопротивление цепи: 1)сопротивление одной лампы мощностью 40Вт составит: R40=U²/P = 12²/40 = 3,6(Ом); 2)сопротивление одной лампы мощностью 60Вт составит: R60=U²/P = 12²/60 = 2,4(Ом); 3)общее сопротивление всех ламп при их последовательном соединении: Rобщ = 3,6*10 + 2,4*10 = 60(Ом); 4)общий той в цепи: Iобщ = U/I = 220/60 = 3.66(A). Следовательно, по закону Ома: 5)напряжение на каждой лампе мощностью 40Вт составит: U40 = Iобщ*R40 = 3.66*3.6 = 13.2(B); 6)напряжение на каждой лампе мощностью 60Вт составит: U60 = Iобщ*R60 = 3.66*2,4 = 8,8(B). Как заметно из результатов вычислений, лампы с меньшей мощностью будут работать с перекалом нити накаливания, а лампы с большей мощностью, наоборот, недокалом. Вывод: при последовательном соединении ламп и составлении из них гирлянд, необходимо брать лампы с полностью одинаковыми параметрами. P.S. При еще большей разнице в мощностях ламп(например, 40Вт и 75Вт) или их количественном соотношении(например 5шт по 40Вт и 15шт по 60Вт)разница в напряжениях может быть еще больше, в результате чего лампы с меньшей мощностью начнут перегорать быстрее. Таким образом, если мы пополним последовательную цепочку из одинаковых ламп какими-нибудь из них отличающимися, то как бы нарушим, если так можно сказать, общее равновесие всей электрической цепи не в пользу менее мощных ламп. Тоже самое произойдет, если в гирлянде из одинаковых новогодних ламп на 13,5В и на 0,16А мы заменим несколько ламп на такое же напряжение, но бОльший ток, например, лампами на 13,5В, но на 0,26А. На менее мощных будет перенапряжение. Поэтому в гирляндах надо использовать только одинаковые лампы - либо по одинаковой мощности и напряжению, либо по одинаковому напряжению и току, смотря какая из этих комбинаций нанесена на корпусе. А вот для параллельного включения ламп данное условие не обязательно. Задача 4.1. Рассчитать общее сопротивление цепи при R1 = 10Ом, R2 = 20Ом, R3 = 30Ом, R4 = 40Ом, R5 = 50Ом, R6 = 60Ом на рис.5.
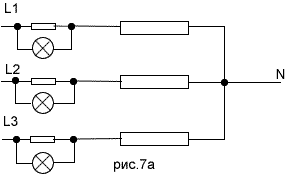
Задача 4.2. Имеется 8 сопротивлений по 10 Ом. Необходимо их все соединить так, чтобы общее сопротивление составило 20 Ом. Решение: Есть два варианта исполнения - либо соединить два сопротивления по 40 Ом параллельно и тогда их общее сопротивление будет равно половине каждого согласно формуле Задача 5.1. На улице установлен щиток со счетчиком. Необходимо из имеющихся в наличии резисторов ПЭВ-100 номиналами 400Ом и 620Ом использовать те, которые смогут обогревать щиток при Решение:Составим схему питания обогревочного резистора(рис.6). Имеющаяся мощность резистора - 100Вт. Поэтому при нагревании выделяющаяся на нем мощность не должна превышать этого значения. Мощность рассчитывается по формуле P = U*I, где U - напряжение питания, I - проходящий через резистор ток. По закону Ома найдем ток, проходящий через резистор по формуле I = U/R. Ток через резистор номиналом 400Ом составит: I1 = 220/400 = 0,55 А. Мощность которая на нем выделится P = U*I1 = 220*0,55 = 121Вт. Этот резистор не подойдет, т.к. реально выделяемая расчетная мощность 121Вт превысит его максимально заданную 100Вт. Задача 5.2. Имеется небольшой водонагреватель для 3-х фазной цепи. Каждый тэн мощностью 1кВт и напряжением 220В. Необходимо на щитке управления смонтировать три лампочки напряжением 1,5В, которые контролировали бы исправность каждого из трех тэнов. Решение: Составим упрощенную схему питания тэнов(рис.7). Чтобы контролировать цепь питания любого тэна, необходимо в цепь его питания последовательно с ним включить такое сопротивление, на зажимах которого образовывалось бы напряжение величиной 1,5В. С него мы и возьмем напряжение на индикаторную лампочку. Величина этого сопротивления определяется согласно закона Ома: R1 = U1/I, где I - величина тока в цепи, R1 - величина искомого сопротивления, U1 - напряжение для лампочки величиною 1,5В. При перегорани тэна цепь питания его лампы оборвется и она погаснет. Рассматриваемая идея представлена на рис.7а. Для упрощения мы пренебрегли полным сопротивлением цепи(исключили маленькое сопротивление), учтя только сопротивление тэна. Получим ток в цепи I = P/U = 1000Вт/220В = 4,55 А. Тогда величина дополнительного сопротивления составит: R1 = U1/I = 1,5/4,55 = 0,33 Ом. Возьмем, к примеру, нихромовую проволоку диаметром 1,5кв.мм(именно такое сечение выдержит такой ток по справочникам - это надо учитывать). Рассчитаем ее необходимую длину по формуле |


 Решение: Данная электрическая цепь является цепью с последовательно включенными проводниками. Общее спротивление тогда рассчитывается по формуле
Решение: Данная электрическая цепь является цепью с последовательно включенными проводниками. Общее спротивление тогда рассчитывается по формуле



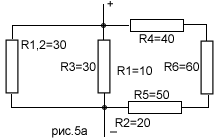
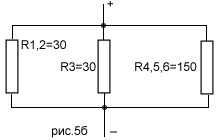 Решение: Найдем общее сопротивление резисторов R1 и R2. Между собою они соединены последовательно. Тогда общее их сопротивление
Решение: Найдем общее сопротивление резисторов R1 и R2. Между собою они соединены последовательно. Тогда общее их сопротивление 
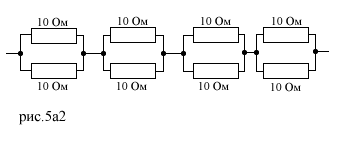 Первый вариант исполнения показан на рис.5а1, второй на рис.5а2.
Первый вариант исполнения показан на рис.5а1, второй на рис.5а2. подаче на них напряжения 220В.
подаче на них напряжения 220В.


 Решение:
Решение: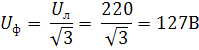

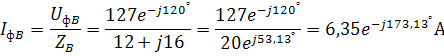

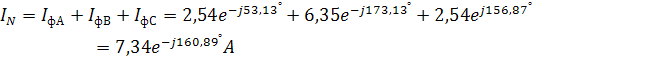
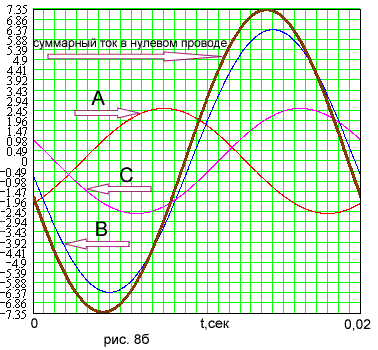

 , т.е.
, т.е.
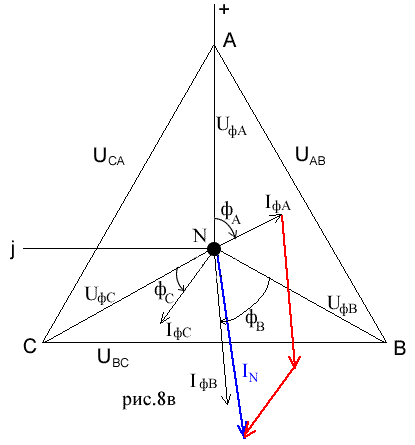
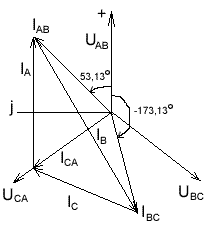 1. Запишем фазные напряжения источника в комплексном виде:
1. Запишем фазные напряжения источника в комплексном виде:


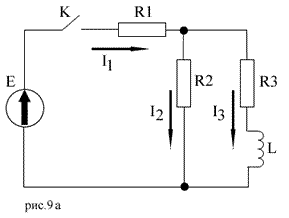
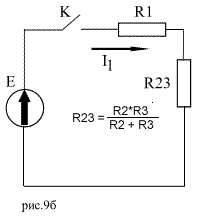 Для решения классическим методом необходимо помнить, что ток в цепи будет состоять из суммы 2-х составляющих токов. Это 1)устоявшийся ток(принудительная составляющая - это одно и тоже), который будет в цепи в результате длительного нахождения ключа в замкнутом состоянии, т.е. когда
Для решения классическим методом необходимо помнить, что ток в цепи будет состоять из суммы 2-х составляющих токов. Это 1)устоявшийся ток(принудительная составляющая - это одно и тоже), который будет в цепи в результате длительного нахождения ключа в замкнутом состоянии, т.е. когда 
 . После приведения к общему знаменателю и математических преобразований получим:
. После приведения к общему знаменателю и математических преобразований получим:
 2.Составим операторную схему замещения. Она на рисунке. По законам Кирхгофа запишем систему:
2.Составим операторную схему замещения. Она на рисунке. По законам Кирхгофа запишем систему: Из второго и третьего уравнений выражаем I2 и I3:
Из второго и третьего уравнений выражаем I2 и I3:
 Подставляя эти значения I2 и I3 в первое уравнение, получим:
Подставляя эти значения I2 и I3 в первое уравнение, получим:
 , где
, где Решение:
Решение: Перепишем их для момента времени t=0:
Перепишем их для момента времени t=0: 



