В разделе "Мощность постоянного тока" было выяснено, что в цепях постоянного тока потребляемая мощность определяется как произведение напряжения и силы тока, а работа как произведение мощности на время. Но вот в цепях переменного тока такой простой расчет невозможен. Если в цепь переменного тока включено только активное сопротивление, такие например, как лампочка, утюг или электрочайник, то полную мощность можно рассчитать как произведение действующего напряжения и тока, которую и покажут нам измерительные приборы, т.е. P=U*I. Такие потребители не содержат индуктивного и емкостного сопротивлений. И, соответственно, работа определяется как A=UIt. Построим для этого случая кривую полной мощности (рис.1).
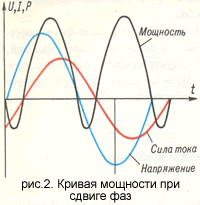
кривая мощностикривая мощностиВ любое время периода мощность положительна, потому как в любое время и напряжение и ток либо положительны, либо отрицательны одновременно. Также говорят, что напряжение и ток совпадают по фазе, либо о нулевом сдвиге фаз между напряжением и током - это одно и тоже. Этот вопрос также рассматривается в разделе "Активное, индуктивное и реактивное сопротивления в цепи переменного тока". Точки на кривой мощности строятся перемножением напряжения и тока в выбранный момент времени.
Однако, случаи нулевого сдвига фаз в цепи переменного тока практически не встречаются из-за наличия в цепях емкостных и индуктивных сопротивлений. Если сопоставить в такой цепи реально имеющуюся активную мощность с мощностью, которую мы получим простым перемножением напряжения и тока при измерении ампервольтомметром(тестером), то мощность, полученная простым перемножением по показанию приборов будет больше реальной активной мощности. Разница между полной мощностью(полученной при перемножении показаний прибора) и используемой активной возникает из-за того, что в электрической цепи всегда имеются индуктивные и емкостные сопротивления, называемые реактивными. А сдвиг фаз между напряжением и током имеет вовсе не нулевое значение. Теперь значения напряжения и тока в один и тот же момент времени могут иметь разные знаки(положительные и отрицательные), а значит и при перемножении может быть мощность отрицательного знака.
Это видно из графика на рис.2. Здесь кривая мощности построена для "отстающего" тока индуктивного характера. Конкретно этот вопрос рассмотрен в разделе "Активное, индуктивное и реактивное сопротивления в цепи переменного тока". Отрицательная мощность объясняется тем, что потребитель тока "возвращает обратно" мощность источнику. Эту мощность называют реактивной.
Реактивная мощность характеризуется обменом энергией между потребителем и источником. Внешне эта энергия не проявляется, но ухудшает полезное действие тока. Реактивная мощность возникает за счет включенных в электрическую цепь катушек индуктивности и конденсаторов.

Итак, необходимо помнить, что переменный ток характеризуется тремя видами мощности.
1) ПОЛНАЯ МОЩНОСТЬ (обозначается как S) - ее можно узнать перемножением действующего напряжения и тока. Это те значения, которые нам показывают амперметр и вольтметр. Кто упустил эту тему - загляните в раздел "Про переменный ток и напряжение". Единица полной мощности - вольт-ампер(ВА);
2)АКТИВНАЯ МОЩНОСТЬ (обозначается как Р) - мощность, которая фактически преобразуется в полезную мощность. Ее-то нам и показывает наш квартирный счетчик.
Единица реактивной мощности - воль-ампер реактивный (вар).
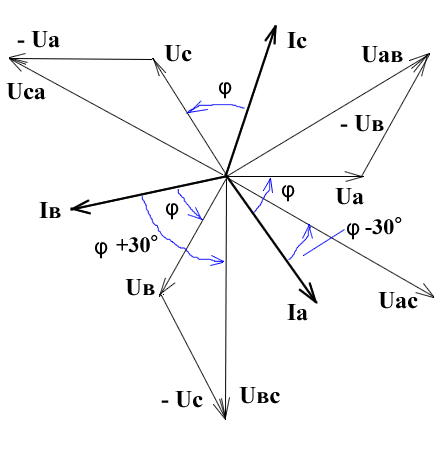
Таким образом, становится ясно, что полный ток состоит из двух составляющих - активного тока и реактивного. Казалось бы, нет ничего проще - сложи их вместе и узнаешь полный ток. Однако, полный ток не является простой суммой двух составляющих. Активный ток имеет одинаковое направление с действующим напряжением, а вот реактивный сдвиинут по фазе на 90° по отношению к активному. Графически полный ток представляют как диагональ прямоугольника, одна из сторон которого представляет собой активную часть тока, а вторая - реактивную (см. рис.3).

умные часы
разложение тока на составляющие

Полный ток, следовательно, получается как геометрическая сумма активной и реактивной составляющих. Численное значение вычисляется как гипотенуза в прямоугольном треугольнике. И если активную часть обозначить как Ia, реактивную как Iр, то получим для полного тока:

I²=I²a + I²p

Из рассмотрения треугольника видно, что реактивная составляющая тем больше, чем больше угол сдвига. Два крайних случая при фазовом угле φ, равном 0 или 90°, практически могут реализоваться толькр в приближении.
При φ = 0 отсутствует реактивная составляющая тока. Активная составляющая и действующий ток равны. Это случай, когда в цепи нет емкостных и индуктивных сопротивлений.
При сдвиге φ=90° (т.е. при чисто индуктивном или емкостном сопротивлении) вовсе нет активной составляющей тока и активной мощности.
Можно легко рассчитать активную Ia и реактивную Iр составляющие тока по действующему значению тока с помощью угла сдвига фаз φ:

cos φ = Ia/I; sin φ = Iр/I; Ia = I*cos φ; Iр = I*sin φ

Для активной мощности записываем: Pa = U*I*cos φ, т.е. чтобы получить активную мощность, необходимо полную мощность S, определяемую как произведение действующих значений U и I, умножть еще на косинус угла сдвига фаз. cos φ называют также "коэффициентом мощности".
Конкретные примеры нахождения мощности переменного тока можно встретить в разделе "Решение задач".

Измерение мощности трехфазной системы

Интересным для некоторых людей представляется вопрос: почему при измерении активной мощности в трехфазной сети достаточно двух ваттметров. Т.е. используется вместе с электросчетчиком не три, а два трансформатора тока.
Тут стоит сразу же заметить, что есть 3-х фазная трехпроводная сеть и трехфазная четырехпроводная сеть. Первая из них в своем составе не имеет нулевого провода, вторая - имеет. Так вот: измерение активной мощности методом двух ваттметров - (применением электросчетчика с подключением всего двух трансформаторов тока) - применяется для трехфазной трехпроводной сети. Чтобы это понять, надо покопаться в законе Кирхгофа и математике. Возьмем классический вариант: питание трехфазной нагрузки, например, электродвигателя. Не вызывает сомнений, что суммарная мощность такой системы равна сумме мощностей всех фаз, а именно:

P = UaIa + UвIв + UcIc

Но в тоже время и сумма всех токов равна нулю, т.е. все три сходятся в одной точке, что по закону Кирхгофа запишется как

Ia + Iв + Ic = 0

Отсюда мы можем выразить, скажем, Ic и подставить значение этого тока в формулу мощности, приведенной выше. Получим:

Ic = - (Ia + Iв) и, соответственно, P = UaIa + UвIв - Uc(Ia + Iв) = UaIa + UвIв - UcIа-UcIв = (Ua - Uc)Ia + (Uв - Uс)Iв

читать далее...
А с учетом того, что разность фазных напряжений (это то, что в скобках) равна соответствующему линейному, т.е. Ua - Uc = Uac, Uв - Uc = Uвс, можно записать, что мгновенная мощность равна
P = UacIa + UвсIв. Этому будет соответствовать первая схема включения из приведенных ниже.

Можно выразить ток Iа. Получим: Iа = - (Iв + Iс) и, соответственно, P = - Ua(Iв + Ic) + UвIв + UcIc = -UaIв - UаIс + UвIв + UcIc = (Uс - Uа)Iс + (Uв - Uа)Iв
А с учетом того, что разность фазных напряжений (это то, что в скобках) равна соответствующему линейному, т.е. Uс - Uа = Uса, Uв - Uа = Uва, можно записать, что мгновенная мощность равна P = UсаIс + UваIв. Этому будет соответствовать вторая схема включения из приведенных ниже.

Можно выразить ток Iв. Получим: Iв = - (Iс + Iа) и, соответственно, P = UaIа - Uв(Iс +Iа) + UcIc = UaIа - UвIс - UвIа + UcIc = (Uа - Uв)Iа + (Uс - Uв)Iс
А с учетом того, что разность фазных напряжений (это то, что в скобках) равна соответствующему линейному, т.е. Uа - Uв = Uав, Uс - Uв = Uсв, можно записать, что мгновенная мощность равна P = UавIа + UсвIс. Этому будет соответствовать третья схема включения из приведенных ниже.
Применять можно любую. Но только в трехпроводной сети. На практике это использование для измерения потребленной электроэнергии двух трансформаторов тока.

Возможные схемы включения двух ваттметров при измерении мощности в 3-х фазной 3-х проводной сети
метод двух ваттметров
метод двух ваттметров
метод двух ваттметров

На основании вышеприведенного получаем, что мгновенная мощность трехфазной трехпроводной сети равна сумме двух произведений мгновенных значений линейных напряжений и токов. Сумма средних значений этих двух произведений, т.е. активная мощность системы, может быть измерена двумя ваттметрами. Для первой схемы включения это
P = P1 + P2 = UcaIacos(φu - φi) + UвсIвcos(φu - φi), где φu - φi - угол сдвига фаз между соответствующими линейным напряжением и током.
При правильном включении ваттметров положительные направления линейных напряжений и токов должны совпадать с направлением от "начала" к "концу" цепи напряжения и цепи тока ваттметров. Так, у первого ваттметра в первой схеме нужно соединить "начало" (вывод, отмеченный звездочкой *) цепи напряжения с проводом А, а "конец" этой цепи - с проводом С.
Распределение измеряемой мощности трехфазной системы между показаниями двух ваттметров зависит главным образом от углов сдвига фаз между линейными напряжениями и токами. Проследим эту зависимость на векторной диаграмме в случае симметричного проемника, фазы которого соединены звездой.

векторная диаграмма при симметричном приемнике
Векторная диаграмма напряжений и токов при симметричной нагрузке
Углы сдвига фаз между соответствующими фазными напряжением и током одинаковые и равны аргументу φ комплексного сопротивления фазы приемника. Из диаграммы следует, что при симметричном приемнике углы сдвига между векторами Uас и Iа (линейным током и линейным напряжением измеряемых ваттметром параметров), Uвс и Iв соответственно равны φ - 30° и φ + 30° . Действующие значения линейных напряжений и токов при симметричном приемнике соответственно одинаковы, т.е. Uвс = Uac = Uл; Ia = Iв = Iл.
Таким образом, сумма показаний двух ваттметров, равна мощности симметричной трехфазной трехпроводной сети, т.е.
P = P1 + P2 = UлIлcos(φ - 30°) + UлIлcos(φ + 30°). Из выражения следует, что при симметричном приемнике показания ваттметров Р1 и Р2 будут равны только при φ = 0. Если φ > 60°, то показание второго ваттметра будет отрицательным, т.е. сумма показаний у них алгебраическая.
Ну, а для измерения в трехфазных системах с нейтральным проводом (4-х проводной) самым простым является метод трех ваттметров. На практике это применение счетчика с тремя трансформаторами тока. При таком подключении каждый измеряет мошность одной фазы и активная мощность такой сети равна
Р = Р1 + Р2 + Р3.