механический резонансмеханический резонансДля понятия явления резонанса можно проделать опыт, показанный на рис.1. К натянутой веревке, прикреплены три пары шариков 1 - 1", 2 - 2", 3 - 3", каждый из которых представляет собой маятник. Если раскачать рукой шарик 1, начинает раскачиваться и шарик 1", а все другие остаются неподвижными. Точно также, если раскачать шарик 3, то начнет качаться шарик 3". Это явление называется механическим резонансом и объясняется следующим образом. Каждый маятник имеет свою собственную частоту колебаний. В нашем случае собственная частота маятников 1 и 1" одинаковая, маятники 2 и 2" тоже имеют одинаковую частоту собсбвенных колебаний и т.д. При раскачивании маятника 1 его колебания передаются по веревке остальным маятникам. Однако, эти колебания раскачивают только маятник 1", частота собственных колебаний которого совпадает с толчками, передающимися по веревке. Поскольку эти толчки производятся в такт с его собственными колебаниями, амплитуда раскачивания этого маятника все больше и больше и может стать больше амплитуды первого маятника. Аналогично этому и явление электрического резонанса.

зависимость контурного тока от частотызависимость напряжения на конденсаторе от частотыНа рис.2 показан лабораторный генератор Г, с помощью которого мы будем подавать высокочастотные колебания различной частоты, но всегда с напряжением 1мВ.
Эти колебания подаются на колебательный контур LC посредством индуктивной связи между катушками Lсв и L. К контуру подключаются приборы для измерения контурного тока и напряжения на конденсаторе. Поскольку L=200мкГн С=500пФ, частота собственных колебаний контура равна 500кГц. Ее значение определяется по формуле Томсона формула Томсона. Если от генератора начать подавать электрические колебания различной частоты, но всегда с напряжением 1мВ, то заметим, что на частоте 500кГц контурный ток и напряжение на конденсаторе сильно нарастают, а на частотах выше и ниже 500кГц они быстро уменьшаются. На рис.3 и рис.4 это явление изображено графически, а кривые называются частотными характеристиками колебательного контура

умные часы
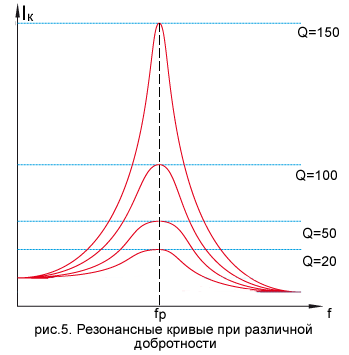
резонансные кривые при различной добротности

Описанное явление объясняется следующим образом. Посредством индуктивной связи в катушке L индуктируется переменная ЭДС, имеющая частоту генератора. В результате в контуре возникают так называемые вынужденные незатухающие электрические колебания (контурный ток) с частотой генератора. В принципе, эти колебания имеют малую амплитуду, т.е. переменное напряжение на конденсаторе намного меньше напряжения генератора. Но когда частота генератора становится равной собственной частоте колебательного контура, наступает явление резонанса. Оно характеризуется тем, что контурный ток значителен и напряжение на конденсаторе может стать во много раз больше (120 - 150 раз) напряжения генератора. Следовательно, колебательный контур обладает так называемой частотной избирательностью и во время резонанса многократно увеличивает напряжение поданных на него колебаний. Чем больше добротность контура, тем больше выражены эти свойства (рис.5).идеальный и реальный колебательный контурСледует отметить, что добротность контура зависит прежде всего от добротности катушки индуктивности, точнее от ее сопротивления потерь. Поэтому иногда реальные колебательные контуры изображаются вместе с сопротивлением потерь катушки индуктивности (рис.6). Видно, что идеальный колебальный контур имеет только емкость и индуктивность. Реальный колебательный контур имеет емкость, индуктивность и сопротивление потерь.
Чем меньше Rпот, тем выше добротность контура. Хорошие колебательные контуры имеют добротность от 50 до 150.
В электрических схемах колебательный контур связан (непосредственно, индуктивно, емкостной связью) с каким-либо источником электрических колебаний. Этим источником может быть антенна, усилительный каскад и другое, которые в общем случае являются генератором с определенным внутренним сопротивлением, частотой и амплитудой. В зависимости от того, как соединен генератор с катушкой индуктивности и конденсатором, различают последовательный и параллельный колебательный контур.

Последовательный колебательный контур

последовательный колебательный контурВ таком контуре генератор соединен последовательно с катушкой и конденсатором. Например, при индуктивной связи колебательный контур последовательный, потому что в катушке (рис.7) индуктируется ЭДС, что равносильно последовательному включению генератора с катушкой L и конденсатором С. Равносильность преобразований показана на рис.7.
Во время резонанса последовательный контур характеризуется следующими особенностями:
1. Сопротивление контура минимально и равно Rпот.
2. Напряжение на конденсаторе (или катушке) в Q раз больше напряжения генератора. Здесь Q - добротность контура.

читать далее...

резонанс напряжений в последовательном контуречастотные характеристики резонанса напряжений3. Ток, протекающий через контур, максимален и равен ток в последовательном контуре.
На рис.8 дан конкретный пример последовательного колебательного контура, а на рис.9 его частотные характеристики при условии, что внутреннее сопротивление генератора невелико.

Таким образом, в последовательном колебальном контуре возникает явление резонанса напряжений. Резонанс напряжений характерен для неразвлетвленного участка цепи, содержащего последовательно соединенные индуктивный, емкостной и резистивный элементы.
Название "резонанс напряжений" отражает равенство действующих значений напряжений на емкостном и индуктивном элементах при противоположных фазах.
Физическая причина возникновения повышенных напряжений - это колебания значительной энергии, запасаемой попеременно в электрическом поле емкостного и в магнитном поле индуктивного элементов. При резонансе напряжений малые количества энергии, поступающей от источника и компенсирующей потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний в системе относительно больших количеств энергии магнитного и электрического полей.

Параллельный колебательный контур

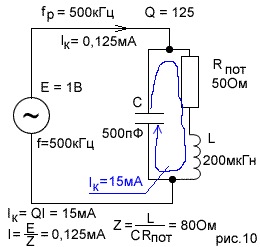
резонанс токов в параллельном контуречастотные характеристики резонанса токовВ этом случае генератор соединен с катушкой индуктивности и конденсатором параллельно. При резонансе параллельный колебательный контур характеризуется следующими особенностями:
1. Сопротивление контура велико и равно L/CRпот (см. рис.10). Это сопротивление иногда называется резонансным сопротивлением параллельного колебательного контура и обозначается Rое.
2. Поскольку сопротивление контура большое, ток во внешней цепи сравнительно мал и равен E/Rое. Контурный ток сравнительно большой. Он в Q раз больше тока во внешней цепи.
На рис.10 дан конкретный пример параллельного колебательного контура и его частотные характеристики, полученные при условии, что внутреннее сопротивление генератора большое.
Таким образом, в параллельном колебательном контуре возникает явление резонанса токов. Резонанс токов характерен для разветвленного участка цепи, содержащего параллельно соединенные конденсатор и индуктивность (через резистор). Либо все три элемента должны быть соединены параллельно. При резонансе токов действующие значения токов в индуктивном и емкостном элементах одинаковые, но противоположны по фазе.