R=100 Ом, C=16мкФ, L=1Гн, U=30В. Найти напряжение и ток на конденсаторе с течением времени.
 Поможите плиз?
Поможите плиз? 
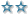
 Поможите плиз?
Поможите плиз? 










Вернуться в «Переходные процессы. Классический метод»
Сейчас этот форум просматривают: нет зарегистрированных пользователей и 10 гостей